TRANSFORMER PROTECTOR
Sole proven solution against transformer explosions. The TP has already saved USD hundreds of millions to transformer owners.
SERGI Transformer Protector
With more than 25 years of expertise, is a worldwide leader in transformer fire and explosion prevention
GOOD FOR SAFETY, ENVIRONMENT, AND REVENUES
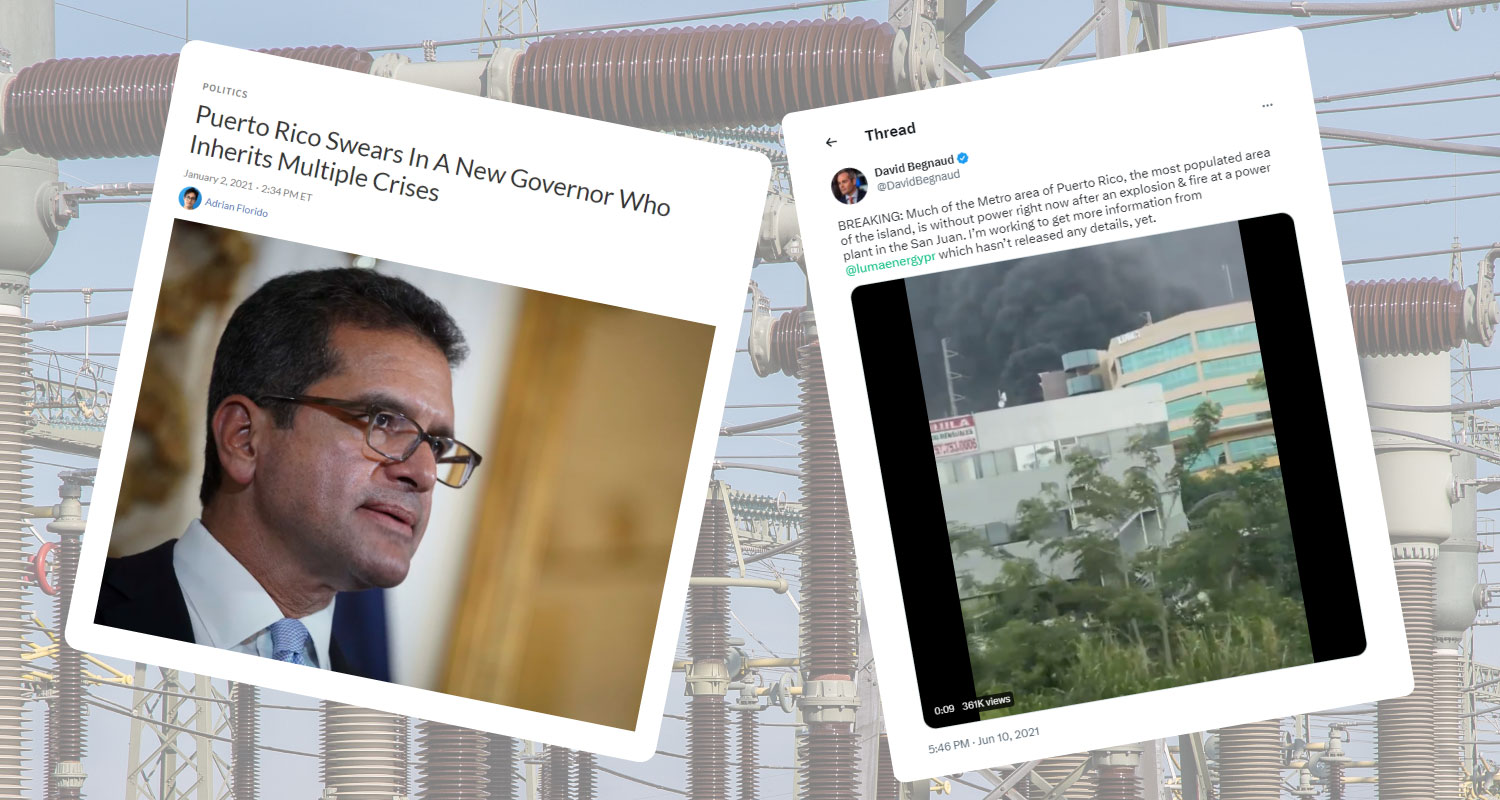
Safeguard your plant infrastructure, secure revenue, and employees´ lives, preventing expensive lawsuits, fines and penalties with the TRANSFORMER PROTECTOR (TP).
INCREASE ELECTRICITY GRID RELIABILITY
The TP is considered by many stakeholders as the solution to increase the high reliability and safety of the electrical grid.
Solutions
Our Activity
As world leader in transformer explosion and fire prevention, we increase our knowledge in transformer explosion phenomena to bring our know-how to the protection of your activity, assets, employees and customers.
Without power, no activity can run. We make sure when a transformer incident occurs that the activity can be back to service 99% faster, as no critical damages have occurred.
Business Segments
Power Generation
Empower your generation plant with advanced protection
Learn morePower Transmission
Shield your powergrid agaist damage and disruptions
Learn moreSpecial Industries
Your critical assets deserve specialized protection
Learn moreInsights & Stories
Find here the best content from us, on key subjects of the energy world
Company
Under the leadership of Electricité de France, SERGI was founded in the years’ 50 to find solution to mitigate risk associated to transformer fires. As a result, the drain and stir system has been developed.
The current SERGI Transformer Protector management has decided to invest in a research program to prevent transformer explosion and its associated fire. In the years 2000, we became the creator of this niche market, answering to the industry’ need of transformer fire prevention.
Since then, SERGI Transformer Protector is the world leader in transformer explosion and fire prevention, with thousands of solutions in operation across more than 80 countries.